Суперперестановка - Superpermutation

В комбинаторный математика, а суперперестановка на п символы - это нить который содержит каждый перестановка из п символы как подстрока. Пока банальный суперперестановки могут быть просто составлены из каждой перестановки, перечисленной вместе, суперперестановки также могут быть короче (за исключением тривиального случая п = 1), потому что допускается перекрытие. Например, в случае п = 2, суперперестановка 1221 содержит все возможные перестановки (12 и 21), но более короткая строка 121 также содержит обе перестановки.
Было показано, что при 1 ≤ п ≤ 5, наименьшая суперперестановка на п символы имеют длину 1! + 2! +… + п! (последовательность A180632 в OEIS ). Первые четыре наименьших суперперестановки имеют соответствующие длины 1, 3, 9 и 33, образуя строки 1, 121, 123121321 и 123412314231243121342132413214321. Однако для п = 5, существует несколько наименьших суперперестановок, имеющих длину 153. Одна такая суперперестановка показана ниже, в то время как другая такой же длины может быть получена переключением всех четверок и пятерок во второй половине строки (после жирного 2):[1]
123451234152341253412354123145231425314235142315423124531243512431524312543121345213425134215342135421324513241532413524132541321453214352143251432154321
Для случаев п > 5, ни малая суперперестановка, ни шаблон для их поиска еще не доказаны, но для них найдены нижняя и верхняя границы.
Поиск суперперестановок
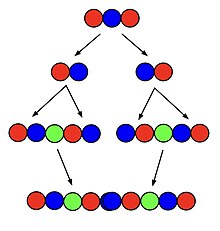
Один из наиболее распространенных алгоритмов создания суперперестановки порядка. рекурсивный алгоритм. Во-первых, суперперестановка порядка разбивается на отдельные перестановки в том порядке, в котором они появились в суперперестановке. Затем каждая из этих перестановок помещается рядом с собственной копией с п-й символ добавлен между двумя копиями. Наконец, каждая результирующая структура размещается рядом друг с другом, и все смежные идентичные символы объединяются.[2]
Например, суперперестановка порядка 3 может быть создана из одной с двумя символами; начиная с суперперестановки 121 и разбивая ее на перестановки 12 и 21, перестановки копируются и размещаются как 12312 и 21321. Они помещаются вместе, чтобы создать 1231221321, а идентичные соседние двойки в середине объединяются, чтобы создать 123121321, что действительно является суперперестановкой порядка 3. Этот алгоритм приводит к кратчайшей возможной суперперестановке для всех п меньше или равно 5, но становится все длиннее самого короткого по мере того, как п увеличиваться сверх этого.[2]
Другой способ найти суперперестановки - создать график где каждая перестановка является вершина и каждая перестановка соединена ребром. Каждое ребро имеет масса связанные с ним; вес рассчитывается исходя из того, сколько символов можно добавить в конец одной перестановки (отбрасывая такое же количество символов с начала), чтобы получить другую перестановку.[2] Например, ребро от 123 до 312 имеет вес 2, потому что 123 + 12 = 12312 = 312. Любое гамильтонов путь через созданный граф является суперперестановкой, и задача нахождения пути с наименьшим весом становится формой задача коммивояжера. Первый экземпляр суперперестановки меньше длины был найден Робином Хьюстоном с помощью компьютерного поиска по этому методу.[3]
Нижняя и верхняя границы
Алгоритм поиска наименьшей суперперестановки для 6 и более символов пока не решен. Однако несколько доказательств постепенно ослабили сильные верхняя и нижняя границы проблемы с течением времени.
Нижние оценки или проблема Харухи
В сентябре 2011 года анонимный плакат о науке и математике ("/ sci /") доска из 4chan доказал, что наименьшая суперперестановка на п символы (п ≥ 2) имеет не менее длины п! + (п−1)! + (п−2)! + п − 3.[4] Что касается японцев аниме серии Меланхолия Харухи Судзумии, проблема была представлена на имиджборде как «Проблема Харухи»: если вы хотите просмотреть 14 серий первого сезона сериала во всех возможных порядке, какую самую короткую последовательность эпизодов вам нужно будет посмотреть?[5] Доказательство этой нижней границы заинтересовало широкую публику в октябре 2018 года после того, как математик и ученый-компьютерщик Робин Хьюстон написал об этом в Твиттере.[4] 25 октября 2018 г. Робин Хьюстон, Джей Пантон и Винс Ваттер опубликовали уточненную версию этого доказательства в Он-лайн энциклопедия целочисленных последовательностей (OEIS).[5][6] В частности, для «Задачи Харухи» (случай для 14 символов) нижняя граница в настоящее время составляет не менее 93 884 313 611, а верхняя - не более 93 924 230 411.[4]
Верхняя граница
20 октября 2018 года, адаптируя конструкцию Аарона Уильямса для строительства Гамильтоновы пути сквозь Граф Кэли из симметричная группа,[7] Грег Иган разработал алгоритм для получения супер-перестановок длины п! + (п−1)! + (п−2)! + (п−3)! + п − 3.[2] До 2018 года это были самые маленькие суперперестановки, известные п ≥ 7. Однако 1 февраля 2019 года Богдан Коанда объявил, что он нашел суперперестановку для n = 7 длиной 5907, или (п! + (п−1)! + (п−2)! + (п−3)! + п - 3) - 1, что стало новым рекордом.[2] 27 февраля 2019 г., используя идеи, разработанные Робином Хьюстоном, Иган произвел суперперестановку для п = 7 длины 5906.[2] Существуют ли аналогичные более короткие суперперестановки для значений п > 7 остается открытым вопросом. Текущая лучшая нижняя граница (см. Раздел выше) для п = 7 по-прежнему 5884.
Смотрите также
- Суперпаттерн, перестановка, содержащая каждую перестановку п символы как шаблон перестановки
- Последовательность де Брюйна, аналогичная задача с циклическими последовательностями
дальнейшее чтение
- Ashlock, Daniel A .; Тиллотсон, Дженетт (1993), "Построение малых суперперестановок и минимальных инъективных суперструн", Congressus Numerantium, 93: 91–98, Zbl 0801.05004
- Анонимный плакат 4chan; Хьюстон, Робин; Пантоне, Джей; Ваттер, Винс (25 октября 2018 г.). «Нижняя граница длины самого короткого супершаблона» (PDF). Он-лайн энциклопедия целочисленных последовательностей.
Рекомендации
- ^ Джонстон, Натаниэль (28 июля 2013 г.). «Неединственность минимальных суперперестановок». Дискретная математика. 313 (14): 1553–1557. arXiv:1303.4150. Bibcode:2013arXiv1303.4150J. Дои:10.1016 / j.disc.2013.03.024. Zbl 1368.05004. Получено 16 марта, 2014.
- ^ а б c d е ж Иган, Грег (20 октября 2018 г.). «Суперперестановки». gregegan.net. Получено 15 января 2020.
- ^ Хьюстон, Робин (21 августа 2014 г.), «Решение проблемы минимальной суперперестановки», arXiv:1408.5108 [math.CO ]
- ^ а б c Григгс, Мэри Бет. «Анонимный пост на 4chan может помочь решить математическую загадку 25-летней давности». Грани.
- ^ а б Кларрайх, Эрика (5 ноября 2018 г.). "Писатель-фантаст Грег Иган и Anonymous Math Whiz продвинули задачу перестановки". Журнал Quanta. Получено 21 июня, 2020.
- ^ Анонимный постер 4chan; Хьюстон, Робин; Пантоне, Джей; Ваттер, Винс (25 октября 2018 г.). «Нижняя граница длины самого короткого супершаблона» (PDF). OEIS. Получено 27 октября 2018.
- ^ Аарон, Уильямс. «Гамильтоничность орграфа Кэли на симметричной группе, порожденной σ = (1 2 ... n) и τ = (1 2)». arXiv:1307.2549v3.
внешняя ссылка
- Проблема минимальной суперперестановки - блог Натаниэля Джонстона
- Грайм, Джеймс. "Суперперестановки - Numberphile" (видео). YouTube. Брэди Харан. Получено 1 февраля 2018.
- Сообщение 4chan на / sci /, заархивировано на warosu.org
- Твитнуть Робин Хьюстон, который привлек внимание к посту 4chan



